在這篇文章中,我們將會展示在 Julia 中使用微分方程解算器(DiffEq solver)搭配神經網路有多麼簡單、有效而且穩定。
Neural Ordinary Differential Equations, 在這篇文章得到 NeurIPS 2018 的最佳論文獎的殊榮之前,其早已成為熱門話題。 這篇論文給出了許多令人讚賞的結果,他結合了兩個不相干的領域,但這只不過是個開始而已: 神經網路與微分方程簡直天生絕配。這篇部落格文章來自 Flux 套件的作者與 DifferentialEquations.jl 套件作者的合作,實作 Neural ODEs 論文, 將會解釋為什麼這個專案會誕生,以及這個專案現在和未來的走向, 也會開始描繪極致的工具會有怎樣的可能性。
Julia 中運用數值方法來解微分方程的 DifferentialEquations.jl 函式庫 的眾多優勢已經在其他文章中被詳細討論。 除了經典 Fortran 方法的眾多效能評測之外, 它包含了其他新穎的功能,像是 GPU 加速、 分散式(多節點)平行運算 以及精密的事件處理。 最近,這些 Julia 土生土長的微分方程方法已經成功地整合進 Flux 深度學習套件, 並允許在神經網路中使用整套完整測試、優化的 DiffEq 方法。 我們將會使用新套件 DiffEqFlux.jl 展示給讀者, 在神經網路中增加微分方程層有多麼簡單,並可以使用一系列微分方程方法, 包含剛性(stiff)常微分方程、隨機微分方程、延遲微分方程,以及混合(非連續)微分方程。
這是第一個完美結合完整微分方程方法及神經網路模型的套件。這個部落格文章將會說明為什麼完整微分方程 方法套組的彈性如此重要。能夠融合神經網路及 ODEs、SDEs、DAEs、DDEs、剛性方程, 以及像伴隨敏感度運算(adjoint sensitivity calculations)這樣不同的方法, 這是一個神經微分方程重大的廣義化工作,將來提供更好的工具讓研究者去探索問題領域。
(註:如果你對這個工作有興趣,同時是大學或是研究所學生, 我們有 提供 Google Summer of Code 專案。 並且 暑假過後有豐厚的津貼補助。 請加入 Julia Slack 的 #jsoc 頻道, 歡迎更進一步的細節討論。)
微分方程究竟與神經網絡有何關聯?
對於不熟悉相關領域的人來說,想必第一個問題自然是:為什麼微分方程在神經網絡這個脈絡下,會有舉足輕重的關聯? 簡而言之,微分方程可以藉由數學模型來敘述、編碼 (encoding) 先驗的結構化假設,來表示任何一種非線性系統。
讓我們稍稍解釋一下最後這句話在說什麼。一般來說,主要有三種方法來定義一個非線性轉換: 直接數學建模、機器學習與微分方程式。 直接數學建模可以直接寫下輸入與輸出間的非線性轉換,但只有在輸入與輸出間的函數關係形式為已知時可用, 然而大部分的狀況,兩者間的確切關係並不是事先知道的。所以大多數的問題是, 你如何在輸入輸出間的關係未知的情況下,來對其做非線性數學建模?
其中一種解決方法是使用機器學習演算法。典型的機器學習處理的問題裡,會給定一些輸入資料 x 和你想預測的輸出 y。 而由給定 \(x\) 產生預測值 \(y\) 就是一個機器學習模型(以下稱作 \(ML\))。 在訓練階段,我們想辦法調整 \(ML\) 的參數讓它得以產生更正確的預測值。 接下來,我們即可用 \(ML\) 進行推論 (即針對事前沒見過的 \(x\) 值去產生相對應的 \(y\))。 同時,這也不過是一個非線性轉換而已 \(y=ML(x)\)。 但是 \(ML\) 有趣的地方在於他本身數學模型的形式可以非常基本但卻可以調整適應至各種資料。 舉例來說,一個簡單的以 sigmoid 函數作為激活函數的神經網路模型(以設計矩陣的形式,design matrix), 本質上來說就是簡單的矩陣運算複合帶入 sigmoid 函數裡。 舉例來說,\(ML(x)=σ(W3⋅σ(W2⋅σ(W1⋅x)))\) 即是一個簡單的三層神經網路模型, 其中 \(W=(W1, W2, W3)\) 為可以被調整的模型參數。 接下來即是選擇適當的 W 使得 \(ML(x)=y\) 可以合理的逼近收集到的資料。 相關機器學習理論已經保證了這是一個估計非線性系統的一個好方法。 舉例來說,Universal Approximation Theorem 說明了只要有足夠的層數或參數(即夠大的 W 矩陣), ML(x) 可以逼近任何非線性函數 (在常見的限制條件下)。
這太好了,它總是有解!然而有幾個必須注意的地方,主要在於這模型需直接從資料裡學習非線性轉換。 但在大多數的狀況,我們並不知曉實際的非線性方程整體,但我們卻可以知道它的結構細節。 舉例來說,這個非線性轉換可以是關於森林裡的兔子的數量,而我們可能知道兔子群體的出生率正比於其數量。 因此,與其從無到有去學習兔子群體數量的非線性模型,我們或許希望能夠套用這個數量與出生率的已知*先驗(a priori)關係, 和一組參數來描寫它。對於我們的兔子群體模型來說,可以寫成
\[\text{rabbits(明日)} = \text{Model}(\text{rabbits(今日)}).\]在這個例子裡,我們得知群體出生率正比於群體數量這個先驗知識。 而如果用數學的方式去描述這個關於兔子群體大小結構的假設,即是微分方程。 在這裡,我們想描寫的事準確地說,是在給定的某一時間點的兔子群體的出生率將會隨著兔子群體大小的增加而增加。 簡單地寫的話,可以寫成以下的式子
\[\text{rabbits}'(t) = \alpha\cdot \text{rabbits}(t)\]其中, \(\alpha\) 是可以學習調整的參數。如果你還記得以前學過的微積分, 這個方程的解即為成長率為 \(\alpha\) 的指數成長函數:
\[\text{rabbits}(t_\text{start})e^{(\alpha t)}\]其中 \(\text{rabbits}(t_\text{start})\) 為初始的兔子數量。但值得注意的是,其實我們並不需要知道這個微分方程的解 才能驗證以下想法:我們只需描寫模型的結構條件,數學即可幫助我們求解出這個解應該有的樣子。 基於這個理由,使得微分方程成為許多科學領域的工具。例如物理學的基本定律明述了電荷的作用力 (馬克士威方程組)。 這些方程組對於物體如何改變是重要的方程組,因此這些方程組的解即是物體將會在哪裡的預測結果。
但在近十年這些應用已經有長遠的發展,隨著像是系統生物學(systems biology)領域的發展, 整合已知的生物結構以及數學上列舉的假設,以學習到關於細胞間的交互作用, 或是系統藥理學(systems pharmacology)中藉由對一些特定藥物劑量 PK/PD 的建模。
所以隨著我們的機器學習模型成長,會渴求更多更大量的資料, 微分方程因此成為一個很有吸引力的選項,用以指定一個可學習(透過參數)但又有限制條件的非線性轉換。 他們會是在整合既有結構關係的領域知識,以及輸入輸出之間很重要的一個方式。 有這樣的方法跟觀點來看待兩者,兩個方法都有其需要取捨的優缺點, 可以讓彼此成為建模上互補的方法。 這看起來是一條開始將科學實踐與機器學習兩相結合的明顯道路,期待未來會有嶄新而令人興奮的未來!
什麼是神經微分方程(ODE)?
神經微分方程只是眾多結合這兩個領域的方法之一。 最簡單的解釋方法就是,並不是直接去學非線性轉換,我們希望去學到非線性轉換的結構。 如此一來,不用去計算 \(y=ML(x)\),我們將機器學習模型放在導數項上 \(y'(x) = ML(x)\),然後我們解微分方程。 為什麼要這麼做?這是因為,一個動機就是這樣定義的模型,然後用最簡單、最容易出錯的方式,尤拉法(Euler method), 解微分方程,你會得到跟殘差神經網路(residual neural network)等價的結果。 尤拉法的工作原理是基於 \(y'(x) = \frac{dy}{dx}\) 這個事實,因此,
\[\Delta y = (y_\text{next} - y_\text{prev}) = \Delta x\cdot ML(x)\]則會導出
\[y_{i+1} = y_{i} + \Delta x\cdot ML(x_{i}) \]這在結構上相似於 ResNet,最為成功的影像處理模型之一。 Neural ODEs 論文的洞見就是,更加深、更加強大的類 ResNet 的模型可以有效地逼近類似於「無限深」, 如同每一層趨近於零的模型。 我們可以直接建構微分方程,不透過增加層數這種手段,隨後用特製的微分方程方法求解。 數值微分方程方法是門可以追溯到第一台電腦出現時期的科學,而現代方法可以動態調整 step sizes \(\Delta x\), 以及使用高階逼近的方法來大幅減少實際需要的步數。並且事實證明,它實務上也運作得很好。
那要怎麼解微分方程呢?
首先,要如何解出微分方程的數值解呢?如果你是解微分方程的新手, 你可能想要參考我們的用 Julia 解微分方程影片教學, 以及參考我們的DifferentialEquations.jl 微分方程教學手冊。 概念是這樣的,如果你透過導函數 u'=f(u,p,t) 定義一個 ODEProblem, 接著就能用初始條件 u0 、時間區段 tspan,以及相關的參數 p 去解這個問題。
舉例來說,洛特卡-沃爾泰拉方程(Lotka-Volterra equations)描述了野兔與狼族群的動態關係。 他們可以被寫成:
\[x^\prime = \alpha x + \beta x y \] \[y^\prime = -\gamma y + \gamma x y \]進一步轉成 Julia 會像:
using DifferentialEquations
function lotka_volterra(du,u,p,t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α*x - β*x*y
du[2] = dy = -δ*y + γ*x*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)然後要解微分方程,你可以簡單地呼叫 solve 來處理 prob:
sol = solve(prob)
using Plots
plot(sol)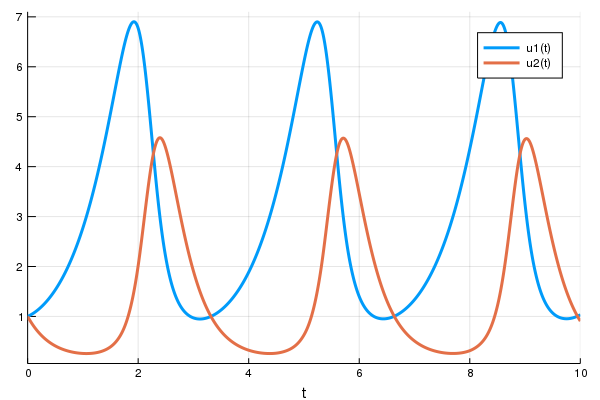
最後一件要說的事情就是我們可以讓我們的初始條件(u0)以及時間區段(tspans) 成為參數(p 的元素)的函式。舉例來說,我們可以這樣定義 ODEProblem:
u0_f(p,t0) = [p[2],p[4
tspan_f(p) = (0.0,10*p[4])
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0_f,tspan_f,p)如此一來,關於這個問題的所有東西都由參數向量決定(p,或是文獻中的 θ)。 這東西的用途會在後續彰顯出來。
DifferentialEquations.jl 提供非常多強大的選項以供客製化, 像是準確度(accuracy)、容忍度(tolerances)、微分方程方法、事件等等;可以參考 手冊以獲得更多進階的使用方式。
讓我們把微分方程放到神經網路架構裡吧!
要理解一個微分方程是怎麼被嵌入到一個神經網路中,那我們就要看看一個神經網路層實際上是什麼。 一個層實際上就是一個可微分函數,它會吃進一個大小為 n 的向量,然後吐出一個大小為 m 的新向量。 就這樣!網路層傳統上是使用簡單的函數,像是矩陣相乘,但有了可微分程式設計的精神, 人們越來越傾向實驗複雜的函數,像是光線追蹤以及物理引擎。
恰巧微分方程方法也符合這樣的架構:一個方法會吃進某個向量 p (它有可能包含一些參數像是初始起點),然後輸出某個新向量,也就是解。 而且它還是可微分的,這代表我們可以直接把他推進大型可微分程式內。 這個大型程式可以開心地容納神經網路,以及我們可以繼續使用標準最佳化技巧, 像是 ADAM 來最佳化那些權重。
DiffEqFlux.jl 讓這件事做起來很簡單;我們一起動手做! 我們就一如往常地開始解這個方程式,不需要計算梯度。
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)
sol = solve(prob,Tsit5(),saveat=0.1)
A = sol[1,:] # length 101 vector我們一起將微分方程的解畫在 (t,A) 座標軸上,一起看看我們得到什麼:
plot(sol)
t = 0:0.1:10.0
scatter!(t,A)
最基礎的微分方程層是 diffeq_rd,它會做相同的事,只有一點語法上的改變。 diffeq_rd 會接受被積函數的參數 p,並且把它放進由 prob 定義好的微分方程中, 然後根據挑選好的程式參數(解算器、容忍度...等等)解方程式。 範例如下:
using Flux, DiffEqFlux
diffeq_rd(p,prob,Tsit5(),saveat=0.1)在 diffeq_rd 中的一個好的設計是,它會處理型別的相容性,讓它可以相容於神經網路框架(Flux)。 要證明這個,我們來用函數定義一層神經網路,然後還有一個損失函數,是輸出值相對 1 距離的平方。 在 Flux 中,他看起來像這樣:
p = param([2.2, 1.0, 2.0, 0.4]) # 初始參數向量
params = Flux.Params([p])
function predict_rd() # 我們的單層神經網路
diffeq_rd(p,prob,Tsit5(),saveat=0.1)[1,:]
end
loss_rd() = sum(abs2,x-1 for x in predict_rd()) # 損失函數現在我們會叫 Flux 來訓練神經網路,藉由跑 100 epoch 來最小化我們的損失函數(loss_rd()), 因此,可以得到最佳化的參數:
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () # 用 callback function 來觀察訓練情況
display(loss_rd())
# 利用 `remake` 來再造我們的 `prob` 並放入目前的參數 `p`
display(plot(solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.1),ylim=(0,6)))
end
# 顯示初始參數的微分方程
cb()
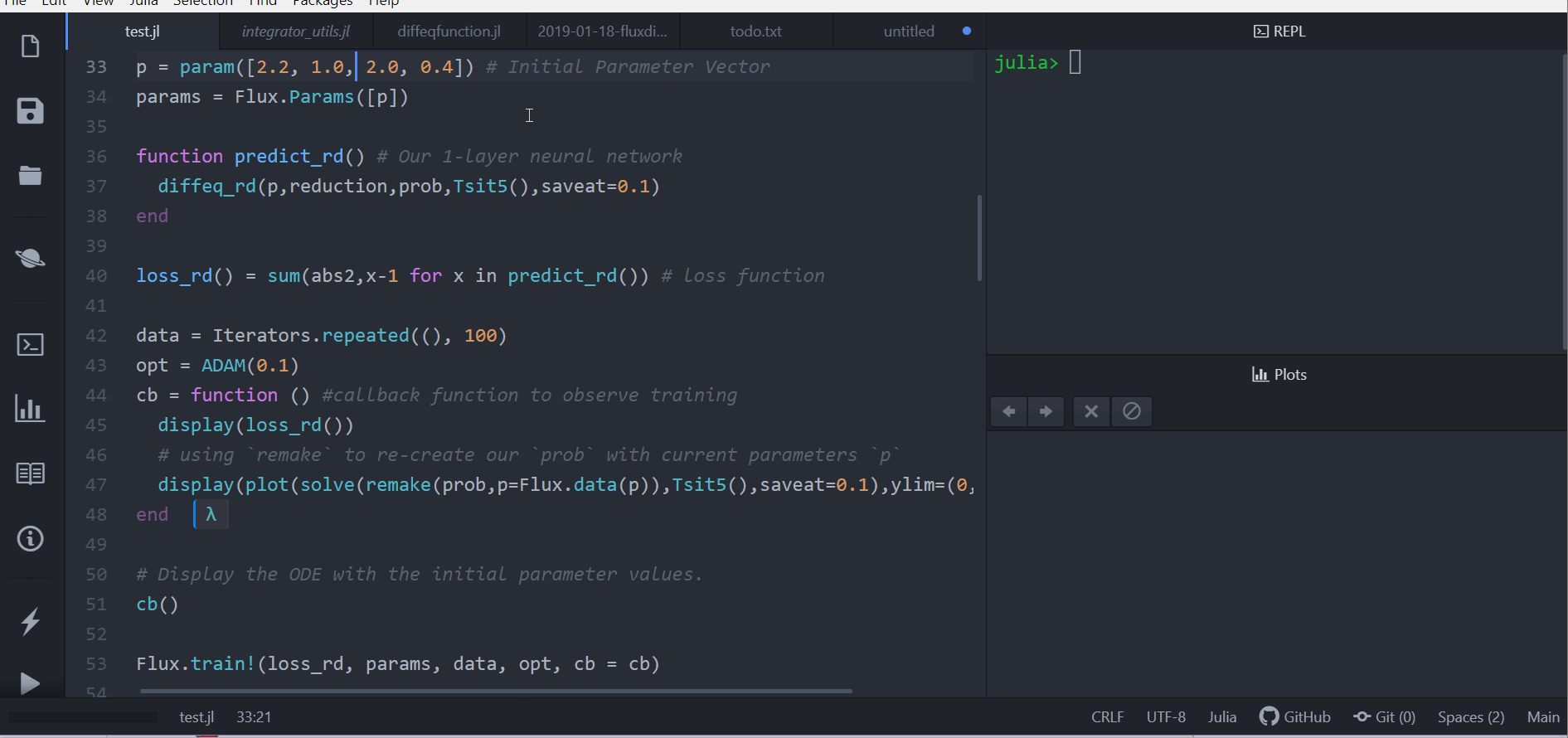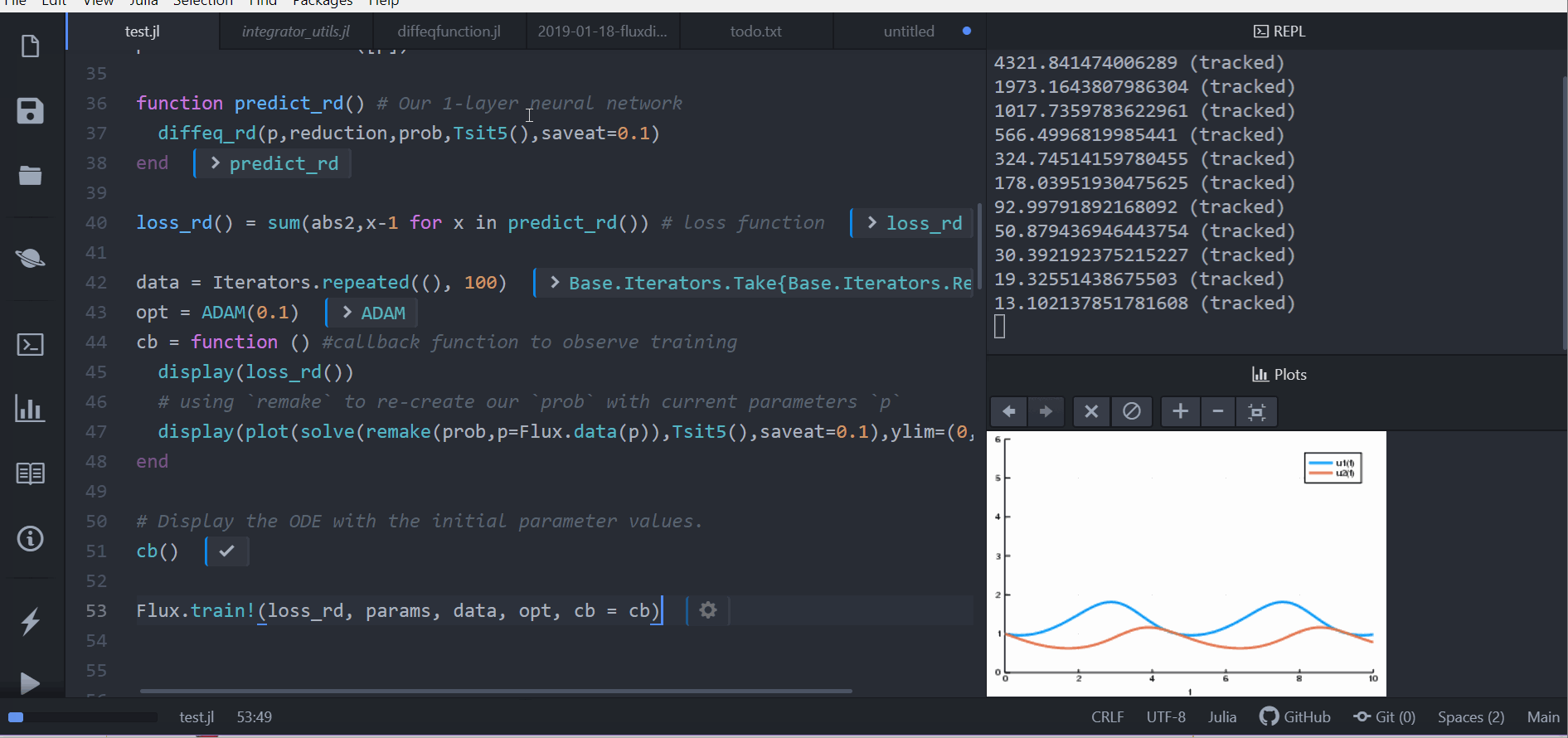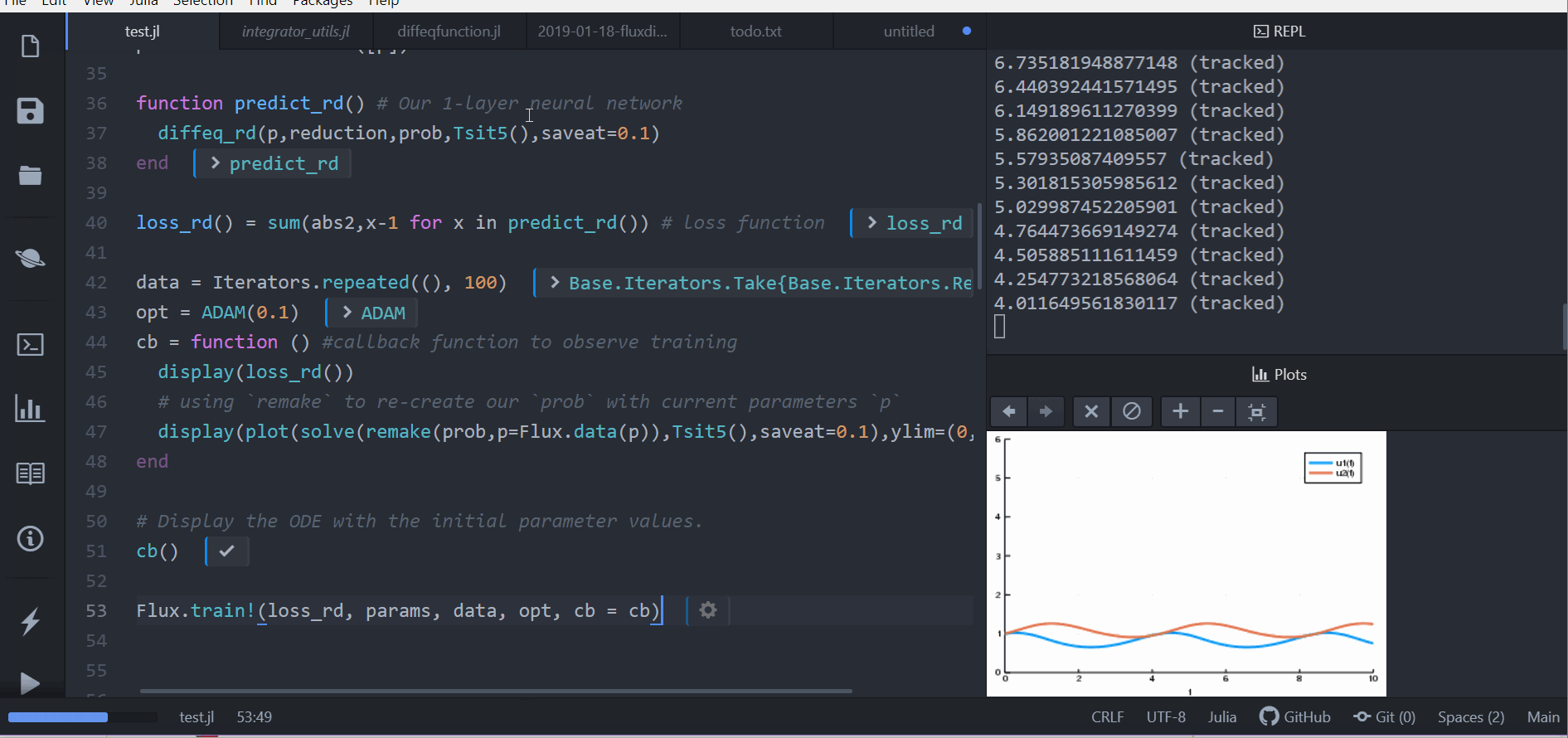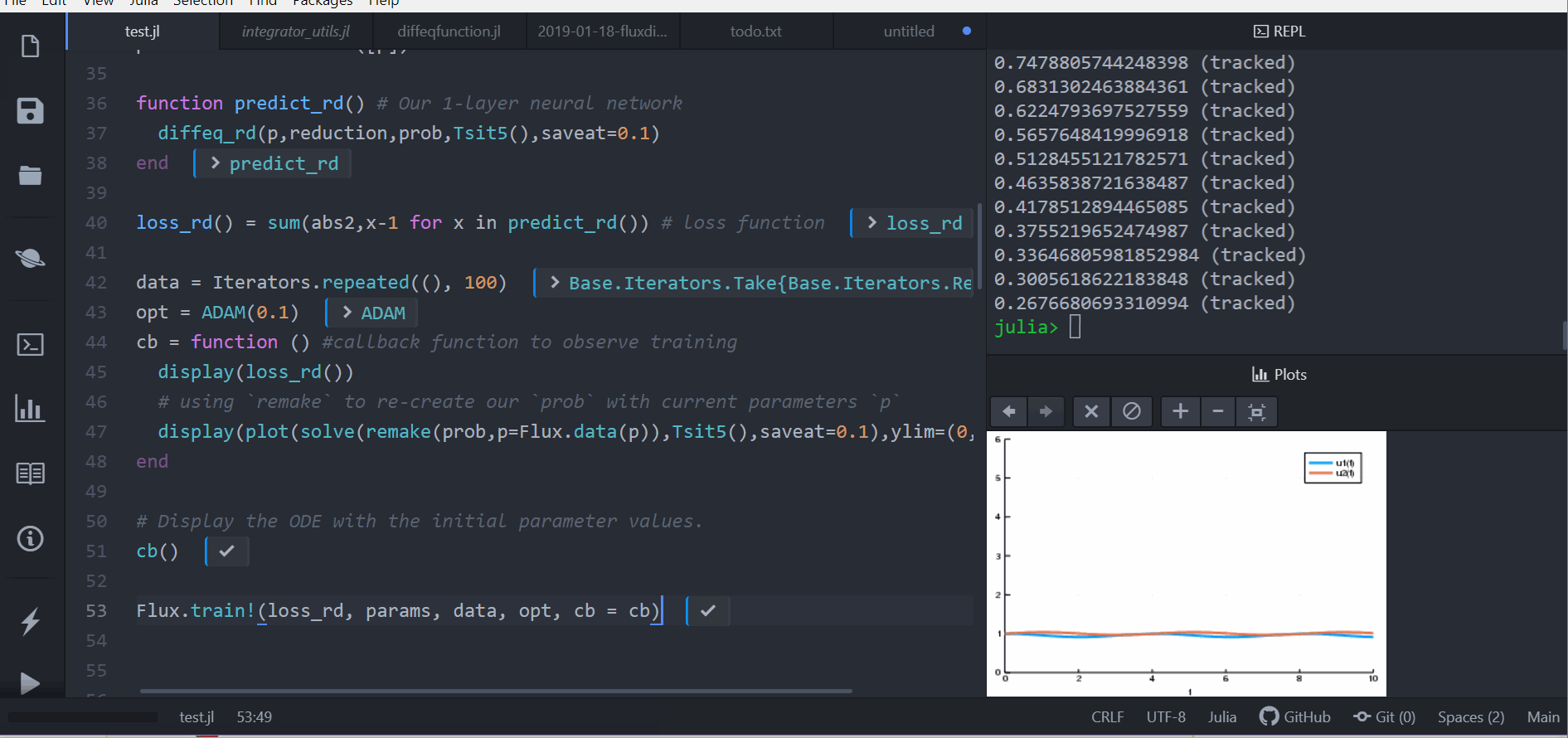
Flux.train!(loss_rd, params, data, opt, cb = cb)結果會以動畫顯示在上面。 這些程式碼會被放在 model-zoo
Flux 在尋找可以最小化損失函數的嗔經網路參數(p),也就是,他會訓練神經網路: 整個過程是這樣的,在神經網路中向前傳遞(forward pass)的過程也包含了解微分方程的過程。 我們的損失函數會懲罰當兔子數量遠離 1 的時候, 所以我們的神經網路會找到兔子以及狼的族群都是常數 1 的時候的參數。
現在,我們已經把微分方程作為一層網路解完了,我們可以隨意將他加到任何地方。 舉例來說,多層感知器(multilayer perceptron)可以用 Flux 寫成像這樣
m = Chain(
Dense(28^2, 32$, relu),
Dense(32, 10),
softmax)而且,假如我們有個帶有合適大小的參數向量的 ODE ,我們可以像這樣把它代入我們的模型中:
m = Chain(
Dense(28^2, 32, relu),
# this would require an ODE of 32 parameters
p -> diffeq_rd(p,prob,Tsit5(),saveat=0.1)[1,:],
Dense(32, 10),
softmax)抑或是,我們也可以把它代入到卷積神經網路中,使用前一層卷積層的輸出當作 ODE 的初始條件使用:
m = Chain(
Conv((2,2), 1=>16, relu),
x -> maxpool(x, (2,2)),
Conv((2,2), 16=>8, relu),
x -> maxpool(x, (2,2)),
x -> reshape(x, :, size(x, 4)),
x -> diffeq_rd(p,prob,Tsit5(),saveat=0.1,u0=x)[1,:],
Dense(288, 10), softmax) |> gpu只要你可以寫下 forward pass,我們就可以處理任何參數化可微分的程序並優化它。一個新世界即為你的囊中之物啊。
完整的 ODE 求解工具對於這個應用為什麼是必須呢?
前文中,我們把現有的求解工具和深度學習結合在一起。反觀另一個傑出的實作 torchdiffeq 採取了另一種實作方式,直接使用 pytorch 實作了許多求解演算法,包含一個適應性的 Runge Kutta 4-5 (dopri5) 和一個 Adams-Bashforth-Moulton 方法 (adams)。然而,其中的實作對於特定的模型來說,雖可算是非常有效率地,但無法完整整合所有可行的求解工具,這帶來了一些限制。
我們考慮以下這個例子:ROBER ODE。最被廣泛測試過 (且最佳化) 過的 Adams-Bashforth-Moulton 方法的實作是著名的 C++ 套件 SUNDIALS 中的 CVODE 積分器 (傳統的 LSODE 的一個分支)。讓我們用 DifferentialEquations.jl 去使用 CVODE 中的 Adams 方法來解這個 ODE 吧:
rober = @ode_def Rober begin
dy₁ = -k₁*y₁+k₃*y₂*y₃
dy₂ = k₁*y₁-k₂*y₂^2-k₃*y₂*y₃
dy₃ = k₂*y₂^2
end k₁ k₂ k₃
prob = ODEProblem(rober,[1.0;0.0;0.0],(0.0,1e11),(0.04,3e7,1e4))
solve(prob,CVODE_Adams())(熟悉使用 MATLAB 解 ODE 的讀者來說,這與 ode113 類似)
包含 Ernst Hairer 的 Fortran 函式庫中的 dopri 在內,這兩種方法在求解這個問題上,都呈現停滯並無法得出結果。其癥結在於,這個 ODE 為“剛性”,而當求解演算法有著「較小的穩定區間」時,將無法對這類 ODE 求解(如讀者想就細節進一步了解的話,我推薦 Hairer 所著的 Solving Ordinary Differential Equations II 一書)。
但另一方面,KenCarp4() 在求解這個問題上,只是一瞬間的事:
sol = solve(prob,KenCarp4())
using Plots
plot(sol,xscale=:log10,tspan=(0.1,1e11))
這不過是個積分法一些微小細節的範例:藉由 PI-適應性控制器和步距預測隱式解算器等,都有著複雜微小的細節並需要長時間的開發與測試,才能變成有效率並穩定的求解器。而不同的問題也會需要不同的方法:如為了在許多物理問題上得到夠好的解並避免偏移,Symplectic 積分器是必須的;另外像是 IMEX 積分器 在求解偏微分方程上也是不可或缺的。由此可見建立一個具產品水準的求解器是有迫切需要,但目前相對稀少的。
在科學運算這個領域,常常會為了機器學習類型的方法設計獨立的函式庫,但在 Julia 中裡兩者並無不同,也就是說你可以直接利用這些現成的函式庫。
究竟有多少種不同的微分方程呢?
常微分方程不過只是其中一種微分方程而已。有許多不同額外的特徵是可以被加入到微分方程的結構式裡。舉例來說,兔子未來數量不是與現在的兔子數量有關,因為親代兔子需要花一段時間懷孕,之後子代兔子才會出生。因此,實際上兔子的出生率應與過去的兔子數量有關。在原來的範例的微分方程中的導數加入一個延遲項,使得這組方程形成所謂的時滯微分方程 (DDE)。由於 DifferentialEquations.jl 使用與常微分方程相同的介面處理時滯微分方程,它也可以被當成 Flux 中的一層神經網路。這裡是個範例:
function delay_lotka_volterra(du,u,h,p,t)
x, y = u
α, β, δ, γ = p
du[1] = dx = (α - β*y)*h(p,t-0.1)[1]
du[2] = dy = (δ*x - γ)*y
end
h(p,t) = ones(eltype(p),2)
prob = DDEProblem(delay_lotka_volterra,[1.0,1.0],h,(0.0,10.0),constant_lags=[0.1])
p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.Params([p])
function predict_rd_dde()
diffeq_rd(p,prob,MethodOfSteps(Tsit5()),saveat=0.1)[1,:]
end
loss_rd_dde() = sum(abs2,x-1 for x in predict_rd_dde())
loss_rd_dde()這個範例的完整程式碼,包含產生動畫在內,可以在 model-zoo 裡找到。
除此之外,我們也可以在微分方程中導入隨機性去模擬隨機事件如何影響預期外的出生或死亡。 這類的微分方程被稱為隨機微分方程 (SDE)。 由於 DifferentialEquations.jl 同樣也可以處理隨機微分方程 (也是目前唯一一個包含剛性與非剛性隨機微分方程解算器的函式庫), 也同樣可以用類似方法引入 Flux 作為神經網路的一層。 以下是使用 SDE 作為神經網路一層的範例:
function lotka_volterra_noise(du,u,p,t)
du[1] = 0.1u[1]
du[2] = 0.1u[2]
end
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,10.0))
p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.Params([p])
function predict_fd_sde()
diffeq_fd(p,sol->sol[1,:],101,prob,SOSRI(),saveat=0.1)
end
loss_fd_sde() = sum(abs2,x-1 for x in predict_fd_sde())
loss_fd_sde()接著我們可以訓練這個神經網路去找出一組參數使得兔子數量成一個定值並觀察中間變化的過程:
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
display(loss_fd_sde())
display(plot(solve(remake(prob,p=Flux.data(p)),SOSRI(),saveat=0.1),ylim=(0,6)))
end
# 畫出當下參數的 ODE
cb()
Flux.train!(loss_fd_sde, params, data, opt, cb = cb)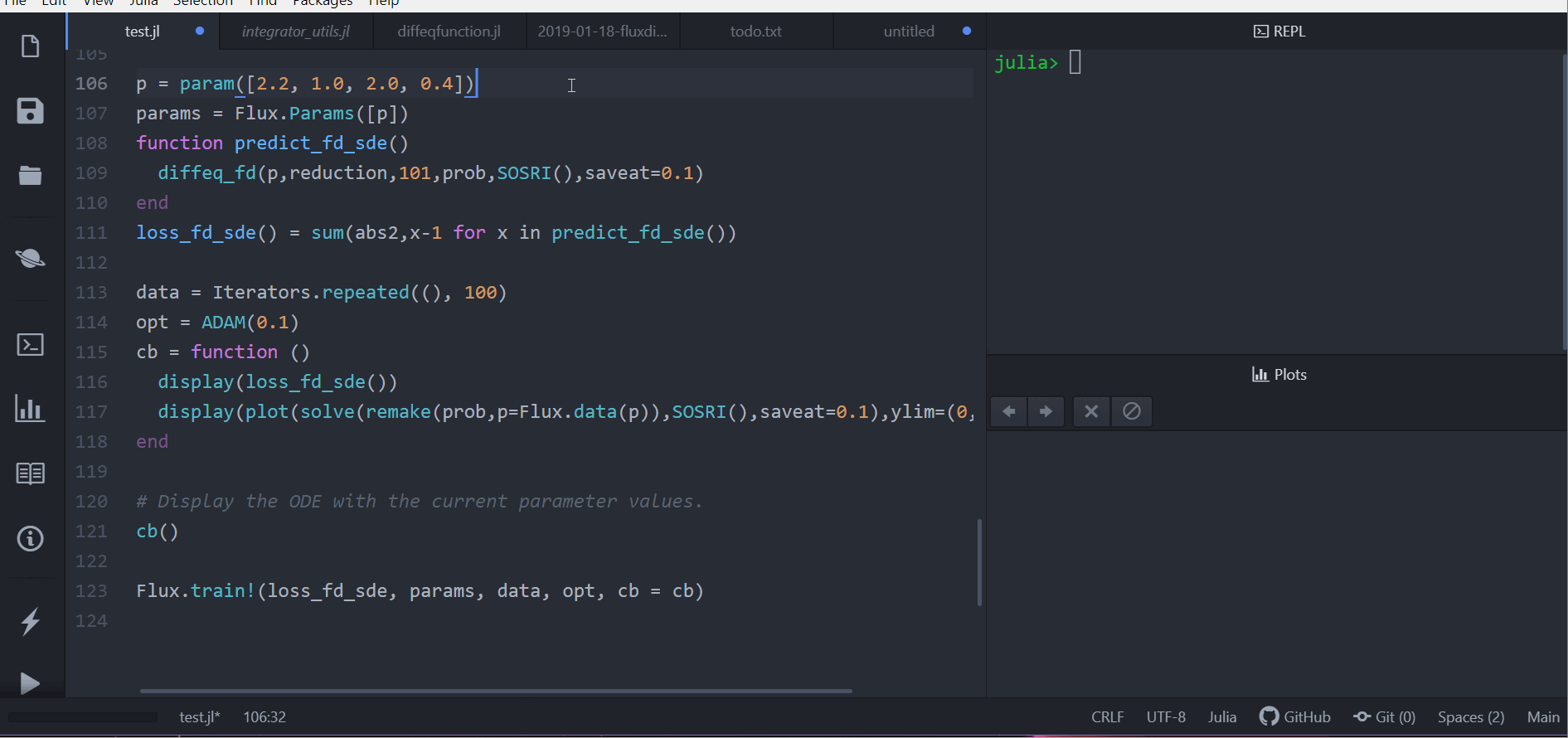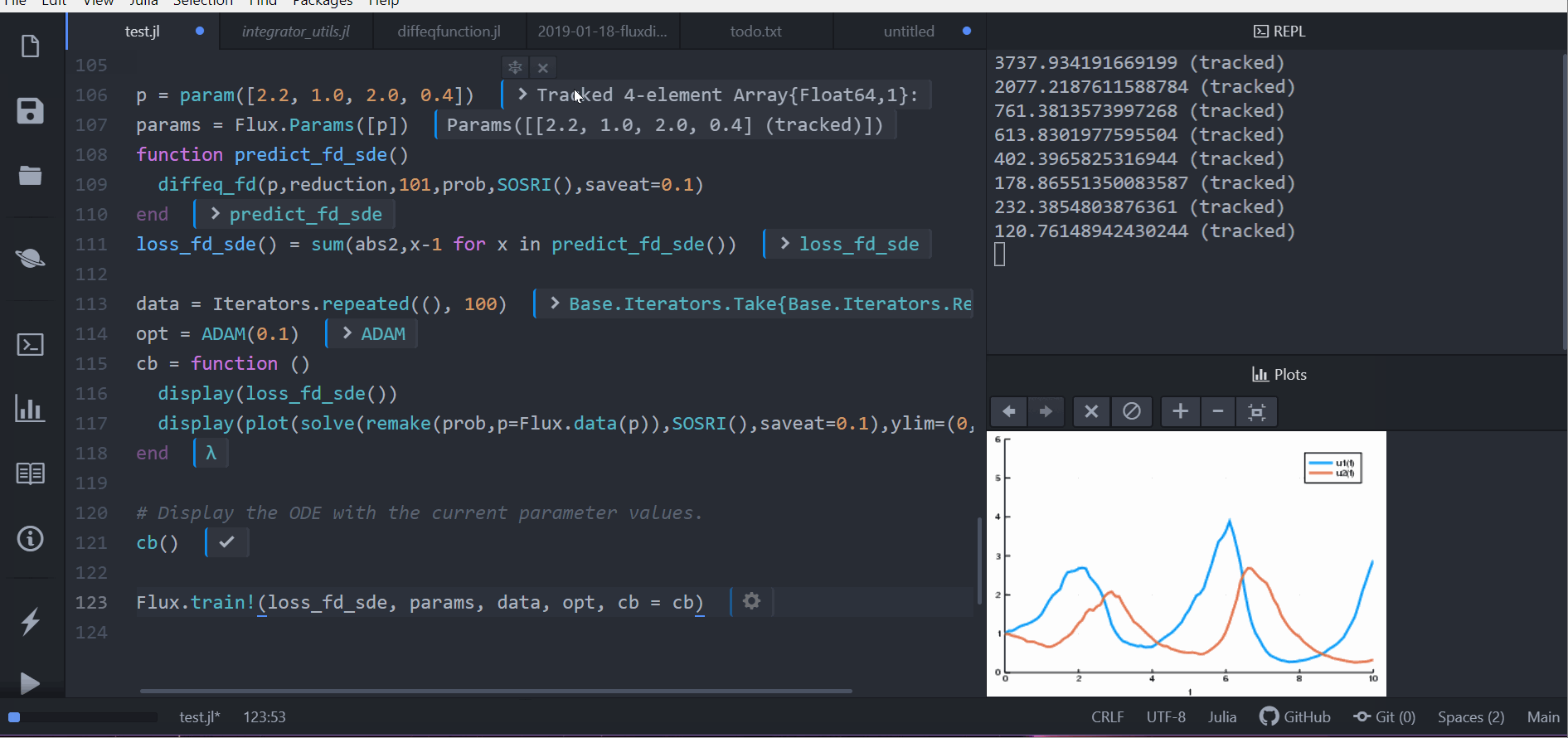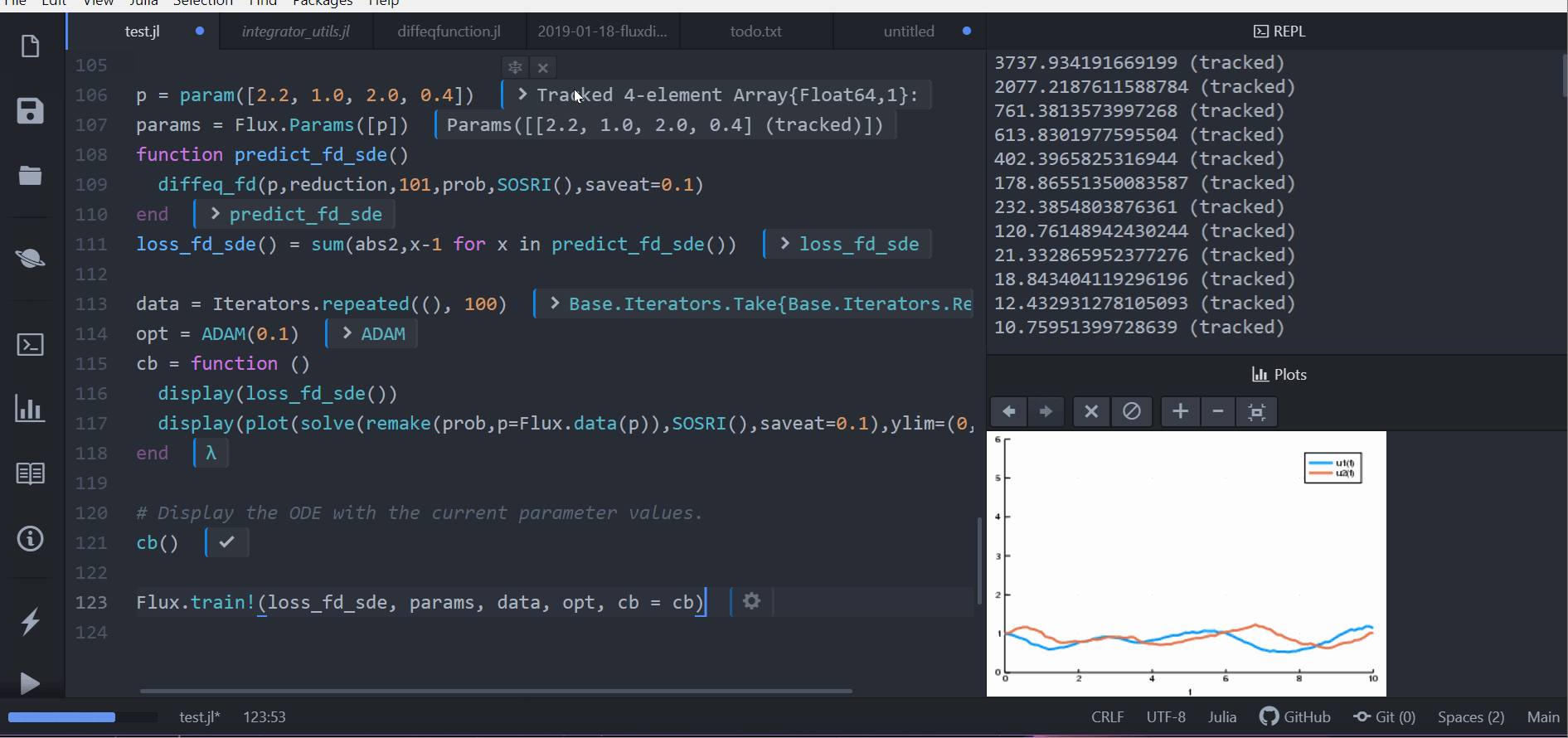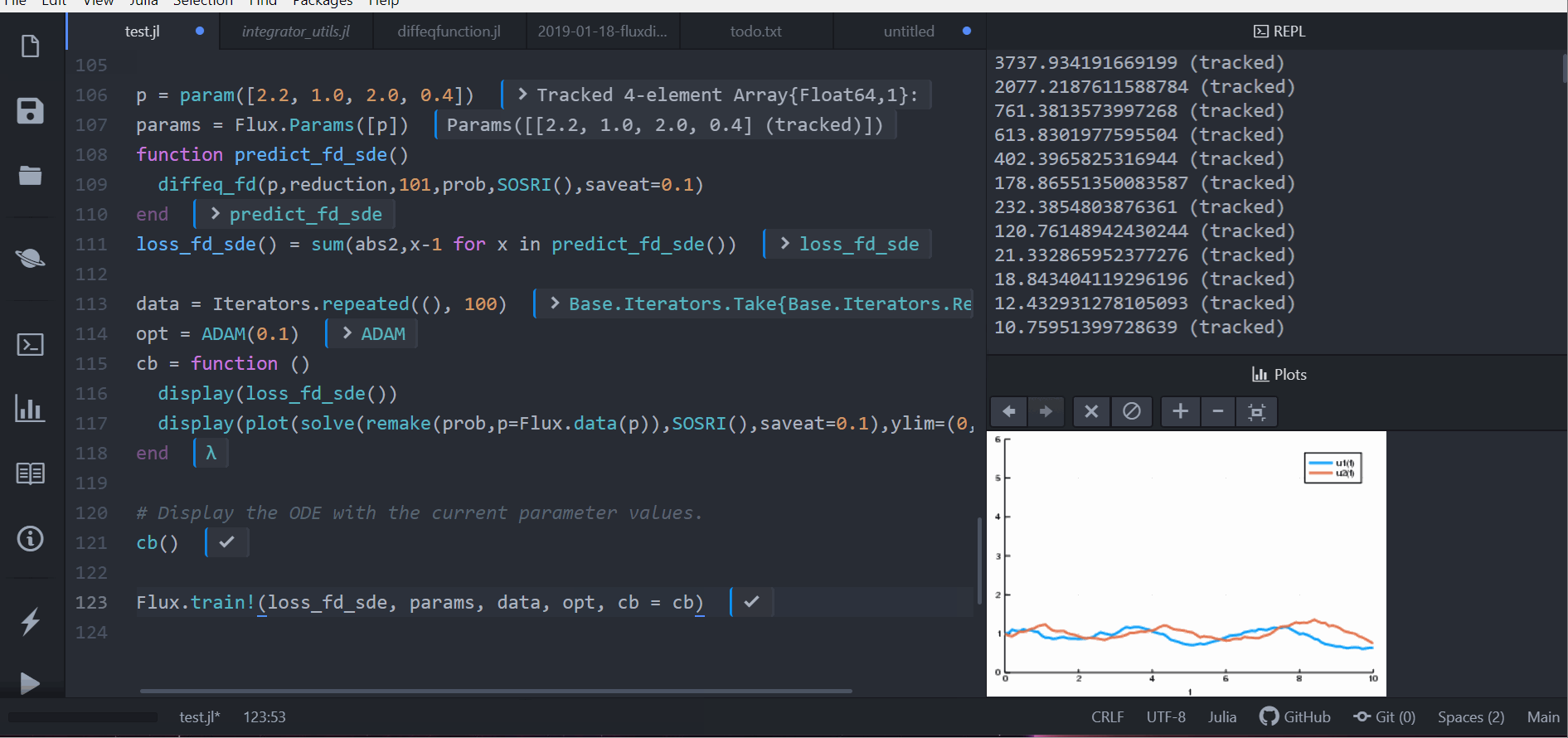
This code can be found in the model-zoo
我們可以繼續下去。譬如也些微分方程式是呈分片段常數函數 (piecewise constant)被使用在生物模擬上,抑或是被應用於財務模型中的跳耀擴散方程式 (jump diffusion)。而上述這些方程式解算器,都可以透過 FluxDiffEq.jl 很好地整合進 Flux 神經網路的架構裡,且 FluxDiffEq.jl 大約只使用了約 100 行左右的程式碼便完成了這些實作。
用 Julia 實作一個常微分方程神經網路層
現在我們回頭用 Julia 實作一個常微分方程神經網路層吧!牢記這不過就是一個把常微分方程中的導數函數替換成一個神經網路層。為此,我們先來定義一個神經網路做為導數。在 Flux 中,我們可以以下的程式碼實作一個多層感知器,帶有一層隱藏層和 tanh 作為 activation function:
dudt = Chain(Dense(2,50,tanh),Dense(50,2))為了定義一個 neural_ode,我們接著定義一個時間跨度並使用 neural_ode 函數如下:
tspan = (0.0f0,25.0f0)
x->neural_ode(dudt,x,tspan,Tsit5(),saveat=0.1)順帶一提,如果想要在 GPU 上運算這個神經網路,只需讓起始條件與神經網路架設於 GPU 上即可。在整合 GPU 的階段,這會使得微分方程解算器內部運算直接在 GPU 上執行,無需額外的資料傳輸。這寫起來會像是[1]:
x->neural_ode(gpu(dudt),gpu(x),tspan,Tsit5(),saveat=0.1)用範例理解常微分神經網路的行為
現在,讓我們用一個例子來看看常微分神經網路層到底是什麼樣子。首先,讓我們用一個常微分方程來產生一個均勻時間點的時間序列。在這裡我們會使用論文中的例子。
u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.5f0)
function trueODEfunc(du,u,p,t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))現在,我們可以用一個常微分神經網路去配適這個資料。為此,我們會定義一個如同上文提及的單層神經網絡(但在這裡我們降低了誤差容忍值來讓模型近似得更接近資料,得以產生較好的動畫):
dudt = Chain(x -> x.^3,
Dense(2,50,tanh),
Dense(50,2))
ps = Flux.params(dudt)
n_ode = x->neural_ode(dudt,x,tspan,Tsit5(),saveat=t,reltol=1e-7,abstol=1e-9)注意到,neural_ode 中使用和產生資料的常微分方程解相同的時間跨度與 saveat,所以它會在每個時間點針對神經網路預測的動態系統狀態來產生一個預測值。讓我們來看看最初這個神經網路會給出怎樣的時間序列。由於這個常微分方程有兩個應變數,為了簡化畫圖的作業,我們只畫出第一個應變數。程式碼如下:
pred = n_ode(u0) # 使用真實的初始值來產生預測值
scatter(t,ode_data[1,:],label="data")
scatter!(t,Flux.data(pred[1,:]),label="prediction")
現在讓我們來訓練我們的神經網路吧!為此,這裡如同前文一般定義了一個預測函數、一個 loss 函數來評估我們的預測值與資料:
function predict_n_ode()
n_ode(u0)
end
loss_n_ode() = sum(abs2,ode_data .- predict_n_ode())接者,我們訓練神經網路,並觀察它如何學習預測我們的時間序列的過程:
data = Iterators.repeated((), 1000)
opt = ADAM(0.1)
cb = function () # 觀察資料用的 callback 函數
display(loss_n_ode())
# 畫出當下預測和資料
cur_pred = Flux.data(predict_n_ode())
pl = scatter(t,ode_data[1,:],label="data")
scatter!(pl,t,cur_pred[1,:],label="prediction")
display(plot(pl))
end
# 呈現初始參數下的常微分方程
cb()
Flux.train!(loss_n_ode, ps, data, opt, cb = cb)
注意到,我們並不是針對 ODE 的解去學習。反而,我們是在學習一個可以產生這組解的小小 ODE 系統。也就是說,這個在 neural_ode 中的神經網路學到的是這個函數:
它學到的是這組時間序列如何運作的一個完整的表示法,並且它可以輕易的使用不同的初始條件對接下來的值進行外插。除此之外,這是個可以學習這樣的表示法非常彈性的架構。舉例來說,如果你的資料有的不是均勻間隔的時間點 t,只需在你的 ODE 解算器中讓 saveat=t,讓解算器去處理這個問題即可。
你可能現在已經猜到了,DiffEqFlux.jl 中還有個其他所有各式各樣額外相關的好東西像是神經隨機微分方程 (neural_msde),讓你去在你的應用中去探索發現。
核心的技術問題:微分方程求解器的反向傳遞
最後,我們來解釋一下為了讓上述理論可行,必須解決的技術問題。 為了要能夠計算損失函數對於網路參數的梯度,任何神經網路架構的核心就是可以去反向傳遞導數。 因此如果我們將一個微分方程求解器作為一個網路層,那麼我們需要反向傳遞通過它。
有很多方法可以實作它。最常見的叫作(伴隨)敏感性分析(adjoint sensitivity analysis)。 敏感性分析定義了一個新的微分方程,它的解會給出損失函數對於參數的梯度, 並且解這個衍生的微分方程。這個方法在 Neural Ordinary Differential Equations 論文中有被討論到, 但事實上,我們將時間倒回到更早之前,當時流行的微分方程求解器框架,像是 FATODE、 CASADI 以及 CVODES 已經使用伴隨法一段時間了(CVODES 甚至從 2005 年就問世了!)。 DifferentialEquations.jl 也提供了敏感性分析的實作。
在伴隨敏感性分析的效率性問題上,它們需要微分方程的多個解。 可預見的,這會非常花時間。像 CVODES 的方法,利用了檢查點機制,藉由儲存接近的時間點來推論解, 伴隨著記憶體用量的增加,得以加速。在 Neural ODE 一文中所使用的方法,則嘗試要以反向的伴隨法來替代對前向方法的依賴。 然而衍生的問題則是,這個方法隱含地假設了微分方程積分器必須是可逆的。 令人失望的是,目前對於一階微分方程尚不存在可逆的適應型積分器,所以沒有這樣的微分方程求解器可以用。 舉例而言,作為一個快速的驗證,在論文中針對這樣的微分方程上使用反向解算器 Adams, 即便設定了 1e-12 的容忍度,還是在最後一個點上就會產生 >1700% 的誤差:
using Sundials, DiffEqBase
function lorenz(du,u,p,t)
du[1] = 10.0*(u[2]-u[1])
du[2] = u[1]*(28.0-u[3]) - u[2]
du[3] = u[1]*u[2] - (8/3)*u[3]
end
u0 = [1.0;0.0;0.0]
tspan = (0.0,100.0)
prob = ODEProblem(lorenz,u0,tspan)
sol = solve(prob,CVODE_Adams(),reltol=1e-12,abstol=1e-12)
prob2 = ODEProblem(lorenz,sol[end],(100.0,0.0))
sol = solve(prob,CVODE_Adams(),reltol=1e-12,abstol=1e-12)
@show sol[end]-u0 #[-17.5445, -14.7706, 39.7985](這邊我們再一次地使用了 SUNDIALS 的 CVODE C++ 求解器, 由於它們最接近於論文中所用的 SciPy 的積分器。)
如此不精確的結果說明了為什麼神經微分方程論文中的方法並不是使用軟體套件中的實作, 這再一次地凸顯了這些小細節。而並非所有微分方程都在這個問題上有如此巨大的誤差。 對於那些並不會造成問題的微分方程來說,伴隨敏感性分析方法會是最有效率的。 除此之外,這個方法只能用於常微分方程上。不只是這樣,它甚至不能被用於所有常微分方程。 舉例來說,具有非連續性(事件)的常微分方程並不符合可微分這個假設。 目前為止,我們再一次得到了相同的總結,單一方法是不夠的。
DifferentialEquations.jl 套件已經實作了非常多不同的方法來計算微分方程的參數微分。 在我們最近的 preprint 文章中,更詳細地描述了這些結果。 我們發現到一件事,直接使用自動微分會是一個最有效而有彈性的方式。 Julia 的 ForwardDiff.jl、Flux,以及 ReverseDiff.jl 套件可以直接將自動微分 用在原生的 Julia 微分方程求解器上,而即使增加新功能也可以提升效率。 我們也證實前向模式自動微分在微分方程少於 100 個參數是最快的, 而對於多於 100 個參數伴隨敏感性分析是最有效率的。 即便如此,我們有好的理由相信次世代反向模式 source-to-source 自動微分,Zygote.jl, 將會是在大量參數下比所有伴隨敏感性分析更為有效率的方式。
總的來說,為了達成擴充性、最佳的、可維護的微分方程及神經網路整合框架, 可以切換不同的梯度方法,而不會改變其餘的程式碼,是一件極其重要的事。 而這正是 FluxDiffEq.jl 要帶給使用者的。當中有三個相似的 API 函式:
diffeq_rd使用了 Flux 的 reverse-mode AD 求解。diffeq_fd使用了 ForwardDiff.jl 的 forward-mode AD 求解。diffeq_adjoint使用了伴隨敏感性分析來「反向傳遞」求解。
然而,要把自動微分的反向模式層切換到前向模式層,只需要改變一個字元即可。 由於基於 Julia 的自動微分可以作用在 Julia 程式碼上, 原生的 Julia 微分方程求解器可以直接從這邊受到助益。
結論
機器學習與微分方程注定是要在一起的,因為他們是在描述非線性世界的互補方法。 在 Julia 的生態中,我們以一種嶄新而獨立的套件整合了微分方程以及深度學習套件, 讓這兩個領域可以直接結合在一起。 由軟體開啟這樣的可能性,目前僅僅是個開端。我們希望未來的部落格文章可以混合兩個領域, 在深度學習框架中能有更深入而酷炫的應用,像是整合我們即將上線的計量藥物(pharmacometric)模擬引擎 PuMaS.jl。 在全方位的微分方程求解器支援 ODEs、SDEs、DAEs、DDEs、PDEs、離散隨機方程等多樣微分方程式下, 我們期待你們將會用 Julia 建構怎樣的次世代的神經網路。
備註:可引用版本將在 Arxiv 上公開。